Review of Optimization

Let’s suppose we want to minimize the following function:

\[ f(x) = x^2. \]

One way to do this is to compute its derivative and find the points where the derivative is zero:

\[ f'(x) = 2x \]

Setting the derivative equal to zero, we find:

\[ 2x = 0 \Rightarrow x = 0 \]

So the minimum of the function is achieved at point x = 0.

But for complex functions, finding the minimum analytically might be particularly hard or even impossible. Here is where the algorithm of gradient descent comes in handy.

Gradient Descent is an optimization algorithm used to find the values of parameters, which minimize a cost function. It’s an iterative approach to finding the minimum of a function.

Here’s how the gradient descent algorithm works:

1. Choose initial guess \(x^{(0)}\) and learning rate \(\alpha\).

2. Update \(x^{(t)}\) with the rule \(x^{(t+1)} = x^{(t)} - \alpha \nabla f(x^{(t)})\) until convergence.

• The intuition behind this algorithm is that we start with a guess for the minimum of the function, and then we move this guess downhill until we reach a point where the gradient is zero, signaling that we have reached a minimum. With a small step size, we should have \(f(x^{(t+1)}) \leq f(x^{(t)})\), so repeating this process should eventually converge to a (local) minimum (or saddle point).

• The learning rate, often denoted by \(\alpha\), is a hyper-parameter that determines the step size at each iteration while moving toward a minimum of a loss function. Also, the \(\nabla\) symbol represents the derivative (also called gradient).

Given our function \(f(x) = x^2\), the update rule becomes:

\[ x^{(t+1)} = x^{(t)} - \alpha * 2 * x^{(t)} \]

From this process, we can pick a point, calculate the gradient at that point, subtract some multiple of the gradient from the point’s coordinates to find the new point, and repeat the process until we find a point where the gradient is near zero, signaling that the minimum of the function has been found.

The advantage of this approach is that we only need to compute the derivative (or gradient) at one point at a time, rather than needing to solve the equation for the derivative equal to zero.

Remember, to use gradient descent effectively, you should probably spend some time tuning the learning rate because if the learning rate is too small, then convergence will be excessively slow, but if the learning rate is too large you might skip the optimal solution or might not converge at all.

In conclusion, that’s how gradient descent algorithm works, a useful iterative method for finding the local minimum of differentiable functions. It provides a general approach to optimizing complex functions, and it’s the backbone of many machine learning algorithms.

Python implementation

import numpy as np

import matplotlib.pyplot as plt
import matplotlib.cm as cm

# define the function
def f(x):
    return x**2

# define the derivative of the function
def df(x):
    return 2*x

# gradient descent function
def gradient_descent(learning_rate, x_start, num_iterations):
    x = x_start
    history = [x] # to store the trajectory of each iteration

    for i in range(num_iterations):
        x = x - learning_rate * df(x) 
        history.append(x)
    
    return history

# parameters
x_start = -5  # initial guess
learning_rate = 0.2
num_iterations = 20

# perform gradient descent
trajectory = gradient_descent(learning_rate, x_start, num_iterations)

trajectory

[-5,
 -3.0,
 -1.7999999999999998,
 -1.0799999999999998,
 -0.6479999999999999,
 -0.3887999999999999,
 -0.23327999999999993,
 -0.13996799999999995,
 -0.08398079999999997,
 -0.05038847999999998,
 -0.030233087999999984,
 -0.018139852799999988,
 -0.010883911679999993,
 -0.006530347007999996,
 -0.0039182082047999976,
 -0.0023509249228799984,
 -0.001410554953727999,
 -0.0008463329722367994,
 -0.0005077997833420796,
 -0.0003046798700052478,
 -0.00018280792200314866]

# plot the function with the trajectory
def plot_function_trajectory(trajectory):
    x = np.linspace(-6, 6, 400)
    y = f(x)

    plt.figure(figsize=[10,5])
    plt.plot(x, y, label=r'$f(x)=x^2$')

    colors = cm.rainbow(np.linspace(0, 1, len(trajectory)))
    plt.scatter(trajectory, [f(i) for i in trajectory], color=colors)

    plt.title('Gradient Descent Optimization')
    plt.xlabel('x')
    plt.ylabel('f(x)')
    plt.legend()
    plt.grid(True)
    plt.show()

plot_function_trajectory(trajectory)

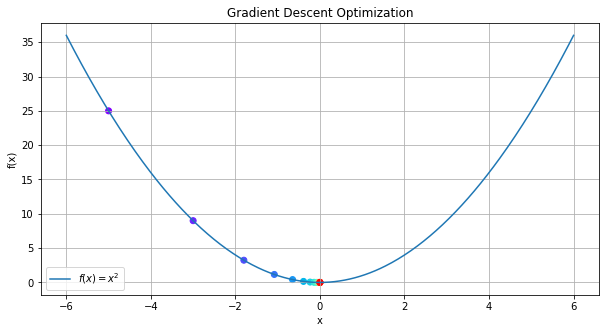
We see that the last point is very close to zero (gradient descent converged to the minimum)

Exercise What happens if we change the learning rate to 0.01?

# parameters
x_start = -5  # initial guess
learning_rate = 0.01
num_iterations = 2000

# perform gradient descent
trajectory = gradient_descent(learning_rate, x_start, num_iterations)

plot_function_trajectory(trajectory)

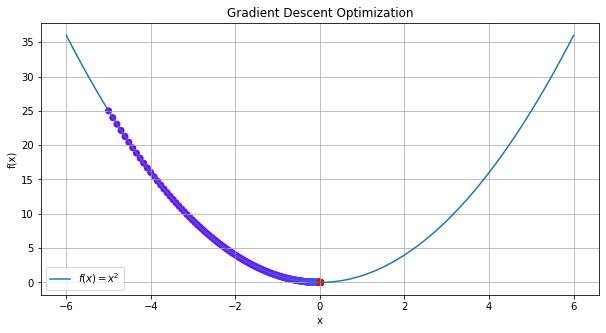
Exercise What happens if we change the learning rate to 1.5?

# parameters
x_start = -5  # initial guess
learning_rate = 1.5
num_iterations = 20

# perform gradient descent
trajectory = gradient_descent(learning_rate, x_start, num_iterations)

plot_function_trajectory(trajectory)

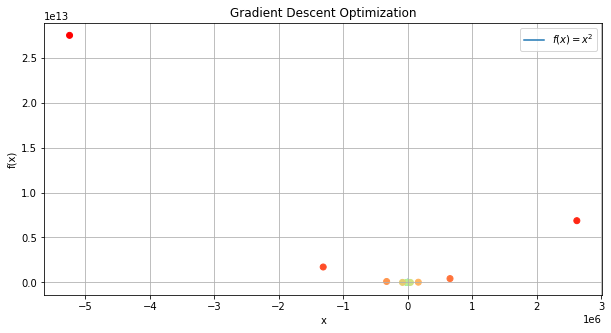
Review of gradients of multivariate functions

The same ideas can be applied to functions of multiple variables. For example, consider the function \(f : \mathbb{R}^3 \rightarrow \mathbb{R}\) defined by:

\[ f(x, y, z) = x^2 + 3y^2 + 5z^2 \]

The gradient of this function is a vector of three components (since the function has three variables), in which each component is the partial derivative of the function with respect that variable. In this case, we have:

$$ \nabla f(x, y, z) = \left( \frac{\partial f}{\partial x}, \frac{\partial f}{\partial y}, \frac{\partial f}{\partial z} \right) = (2x, 6y, 10z)

Note: Since the gradient has the same number of components as the inputs of the function, we can still apply the same idea of gradient descent to find the minimum of the function. The only difference is that now we need to update all the components of the input vector at the same time. For example, if we start with an initial guess \((x^{(0)}, y^{(0)}, z^{(0)})\), then the update rule becomes:

\[ (x^{(t+1)}, y^{(t+1)}, z^{(t+1)}) = (x^{(t)}, y^{(t)}, z^{(t)}) - \alpha \nabla f(x^{(t)}, y^{(t)}, z^{(t)}) \]

Automatic Differentiation

Automatic Differentiation (AD), also known as algorithmic differentiation or computational differentiation, is a set of techniques to numerically evaluate the derivative of a function specified by a computer program.

AD exploits the fact that every computer program, no matter how complex, executes a sequence of elementary arithmetic operations such as addition, subtraction, multiplication, division, etc., and elementary functions such as exp, log, sin, cos, etc. By applying the chain rule repeatedly to these operations, derivatives of arbitrary order can be computed automatically, accurately to working precision, and using at most a small constant factor more arithmetic operations than the original program.

The most popular libraries for AD are TensorFlow and PyTorch.

• TensorFlow, developed by Google https://www.tensorflow.org

• PyTorch, developed by Meta (Facebook) https://pytorch.org

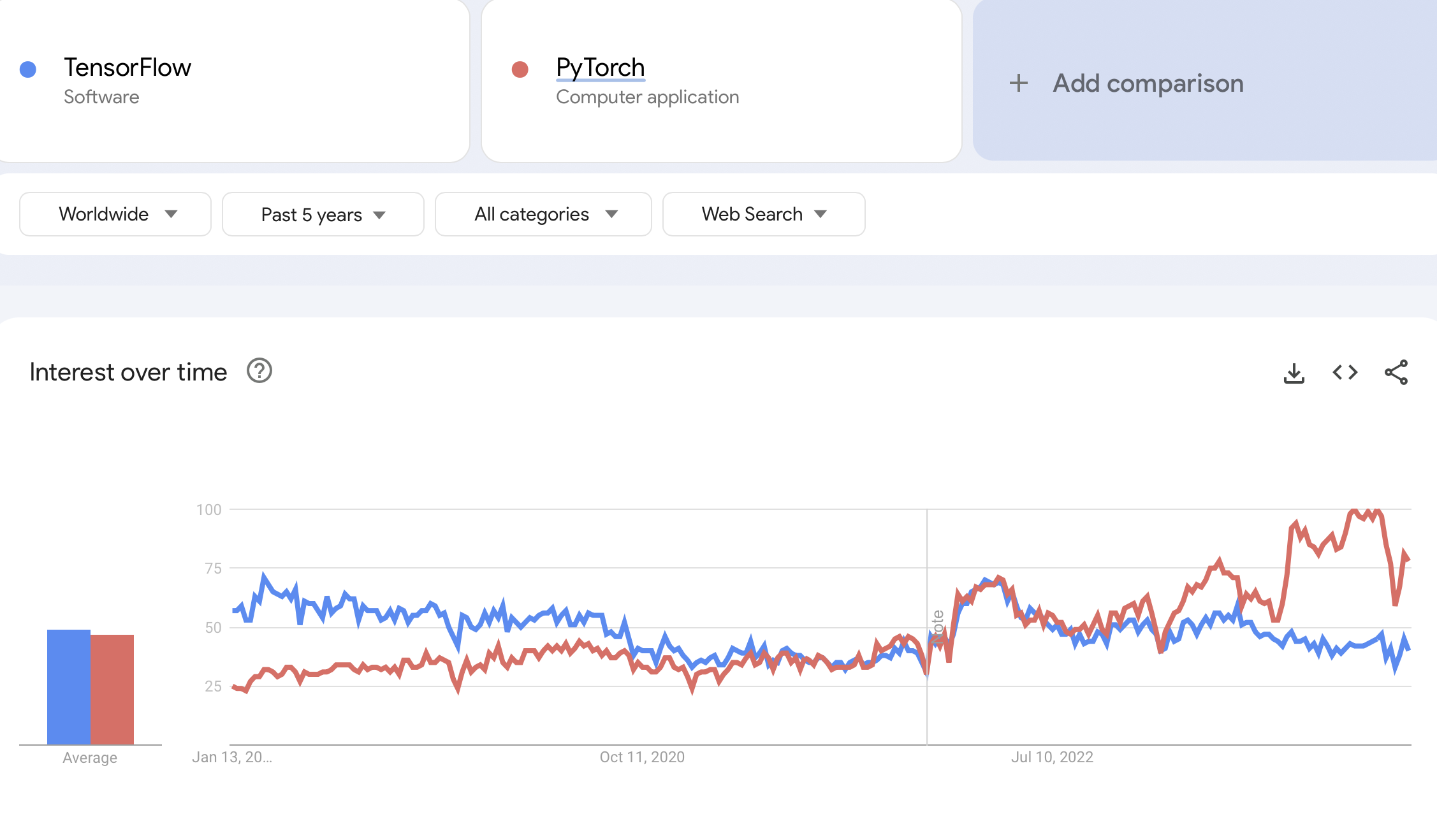
In this course, we will mainly focus on Pytorch, since it is more flexible and has gained more popularity in the recent years (which means more support).

You can install following the instructions in the official website:

https://pytorch.org/get-started/locally/

which typically just involves running the following command:

pip install torch

import torch
import numpy as np

Tensors

Tensors are the PyTorch equivalent to Numpy arrays, with the addition to also have support for automatic differentiation (more on this later). The name “tensor” is a generalization of concepts you already know. For instance, a vector is a 1-D tensor, and a matrix a 2-D tensor. When working with neural networks, we will use tensors of various shapes and number of dimensions.

Most common functions you know from numpy can be used on tensors as well.

x = torch.Tensor([[1, 2], [3, 4]])
x

tensor([[1., 2.],
        [3., 4.]])

x = torch.zeros(10)
x

tensor([0., 0., 0., 0., 0., 0., 0., 0., 0., 0.])

x = torch.randn(3, 3)
x

tensor([[ 0.9499, -0.2473, -0.4399],
        [-0.8217,  1.3747, -0.7969],
        [-0.5173,  0.9696,  0.3041]])

You can obtain the shape of a tensor in the same way as in numpy (x.shape)

x.shape

torch.Size([3, 3])

Tensor to Numpy, and Numpy to Tensor

Tensors can be converted to numpy arrays, and numpy arrays back to tensors. To transform a numpy array into a tensor, we can use the function torch.from_numpy:

np_arr = np.array([[1, 2], [3, 4]])
tensor = torch.from_numpy(np_arr)

print("Numpy array:", np_arr)
print("PyTorch tensor:", tensor)

Numpy array: [[1 2]
 [3 4]]
PyTorch tensor: tensor([[1, 2],
        [3, 4]])

To transform a PyTorch tensor back to a numpy array, we can use the function .numpy() on tensors:

tensor = torch.arange(4)
np_arr = tensor.numpy()

print("PyTorch tensor:", tensor)
print("Numpy array:", np_arr)

PyTorch tensor: tensor([0, 1, 2, 3])
Numpy array: [0 1 2 3]

Operations and Indexing

Most operations that exist in numpy, also exist in PyTorch. A full list of operations can be found in the PyTorch documentation, https://pytorch.org/docs/stable/tensors.html#

x1 = torch.rand(2, 3)
x2 = torch.rand(2, 1)  # notice the broadcasting in the last dimension, similar to numpy

y = x1 + x2
y

tensor([[1.1162, 0.7587, 0.7166],
        [1.1841, 1.4881, 1.7161]])

We often have the situation where we need to select a part of a tensor. Indexing works just like in numpy, so let’s try it:

y[0:2, 0:1]  # first two rows, first column

tensor([[1.1162],
        [1.1841]])

# it's the same as 
# (you can avoid writing the 0's)
y[:, :1]

tensor([[1.1162],
        [1.1841]])

Automatic Differentiation with PyTorch

One of the main reasons for using PyTorch in Machine/Deep Learning is that we can automatically get gradients/derivatives of functions that we define. We will mainly use PyTorch for implementing neural networks, and they are just fancy functions.

The first thing we have to do is to specify which tensors require gradients. By default, when we create a tensor, it does not require gradients:

x = torch.ones(3)
print(x.requires_grad)

False

We can change this for an existing tensor using the function requires_grad_(). Alternatively, when creating a tensor, you can pass the argument `requires_grad=True`` to most initializers we have seen above.

# these two are the same:
x = torch.ones(3, requires_grad=True)
x

tensor([1., 1., 1.], requires_grad=True)

x = torch.ones(3)
x.requires_grad_(True)

tensor([1., 1., 1.], requires_grad=True)

Let’s say we now want to compute the gradient of the function

\[ y = f(x) = \sum_{i=0}^2 (x_i + 1)^2 \]

with respect to the input \(x = (x_0, x_1, x_2) = (1, 1, 1)\in \mathbb{R}^3\).

We can do this automatically as follows:

1. Let’s build the operations that define the function \(f(x)\) step by step:

a = x + 1  # add 1 to each element of the vector x
b = a ** 2 # square each element of the vector a
# now we sum all the components:
y = b.sum()

y

tensor(12., grad_fn=<SumBackward0>)

So \(f((1, 1, 1)) = 12\).

But what we really want is the derivative: \(\nabla_x f((1, 1, 1))\).

2. Call the backward method on the output tensor (it computes the gradient of all the variables using the chain rule):

y.backward()

3. Now we can access the gradient of \(f\) with respect to \(x\) by calling the grad attribute of \(x\):

x.grad

tensor([4., 4., 4.])

So there is no need to compute the derivatives by hand, PyTorch does it for us!

Exercise: Compute \(\nabla_x f((0, 1, 2))\)

x = torch.Tensor([0., 1, 2])
x.requires_grad_(True)

a = x + 1  # add 1 to each element of the vector x
b = a ** 2 # square each element of the vector a
# now we sum all the components:
y = b.sum()
y

tensor(14., grad_fn=<SumBackward0>)

y.backward()

print("The gradient is",x.grad)

The gradient is tensor([2., 4., 6.])

Exercise: Compute \(\nabla_x f^2((0, 1, 2))\)

x = torch.Tensor([0., 1, 2])
x.requires_grad_(True)

a = x + 1  # add 1 to each element of the vector x
b = a ** 2 # square each element of the vector a
# now we sum all the components:
y = b.sum()**2
y

tensor(196., grad_fn=<PowBackward0>)

y.backward()

x.grad

tensor([ 56., 112., 168.])

Some models in PyTorch

Linear Regression

We are given a set of data points \(\{ (x_1, t_1), (x_2, t_2), \dots, (x_N, t_N) \}\), where each point \((x_i, t_i)\) consists of an input value \(x_i\) and a target value \(t_i\).

The model we use is: $\( y_i = wx_i + b \)$

We want each predicted value \(y_i\) to be close to the ground truth value \(t_i\). In linear regression, we use squared error to quantify the disagreement between \(y_i\) and \(t_i\). The loss function for a single example is: $\( \mathcal{L}(y_i,t_i) = \frac{1}{2} (y_i - t_i)^2 \)$

We can average the loss over all the examples to get the cost function: $\( \mathcal{C}(w,b) = \frac{1}{N} \sum_{i=1}^N \mathcal{L}(y_i, t_i) = \frac{1}{N} \sum_{i=1}^N \frac{1}{2} \left(wx_i + b - t_i \right)^2 \)$

Remember that the goal of training is to find the values of \(w\) and \(b\) that minimize the cost function \(\mathcal{C}(w,b)\).

Data generation

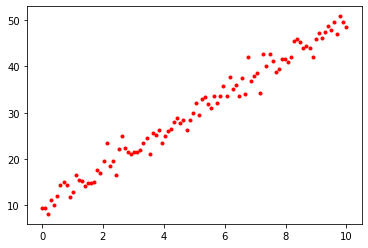
We generate a synthetic dataset \(\{ (x_i, t_i) \}\) by first taking the \(x_i\) to be linearly spaced in the range \([0, 10]\) and generating the corresponding value of \(t_i\) using the following equation (where \(w = 4\) and \(b=10\)): $\( t_i = 4 x_i + 10 + \epsilon \)$

Here, \(\epsilon \sim \mathcal{N}(0, 2)\) (that is, \(\epsilon\) is drawn from a Gaussian distribution with mean 0 and variance 2). This introduces some random fluctuation in the data, to mimic real data that has an underlying regularity, but for which individual observations are corrupted by random noise.

import numpy as np
import torch
import matplotlib.pyplot as plt

# In our synthetic data, we have w = 4 and b = 10
N = 100  # Number of training data points
x = np.linspace(0, 10, N)

t = 4 * x + 10 + np.random.normal(0, 2, x.shape[0])
plt.plot(x, t, "r.")

x = torch.from_numpy(x)
t = torch.from_numpy(t)

Gradient descent

# Initialize random parameters
w = torch.randn(1, requires_grad=True)
b = torch.randn(1, requires_grad=True)

# define cost function
def cost(w, b):
    y = w * x + b
    return (1 / N) * torch.sum( (y - t) ** 2)


# Find the gradient of the cost function using pytorch
num_iterations = 1000 # Number of iterations
lr = 0.01  # Learning rate

for i in range(num_iterations):

    # Evaluate the gradient of the current parameters stored in params
    loss = cost(w, b)
    loss.backward()

    if i % 100 == 0:
        print(f"i: {i:<5d} loss: {loss.item():.4f}")

    # Update parameters w and b
    with torch.no_grad():

        w.data = w - lr * w.grad
        b.data = b - lr * b.grad

        w.grad.zero_()  # we set the gradients to zero before the next iteration
        b.grad.zero_()

i: 0     loss: 1083.7414
i: 100   loss: 10.4761
i: 200   loss: 5.7141
i: 300   loss: 3.9540
i: 400   loss: 3.3034
i: 500   loss: 3.0629
i: 600   loss: 2.9740
i: 700   loss: 2.9412
i: 800   loss: 2.9290
i: 900   loss: 2.9246

Seems that the loss has converged to some minimum. Let’s see what the values of \(w\) and \(b\) are:

w, b

(tensor([4.0257], requires_grad=True), tensor([9.8727], requires_grad=True))

# Plot the training data again, together with the line defined by y = wx + b
# where w and b are our final learned parameters
b_numpy = b.detach().numpy()
w_numpy = w.detach().numpy()

plt.plot(x, t, "r.")
plt.plot([0, 10], [b_numpy, w_numpy * 10 + b_numpy], "b-")

[<matplotlib.lines.Line2D at 0x15e70f220>]

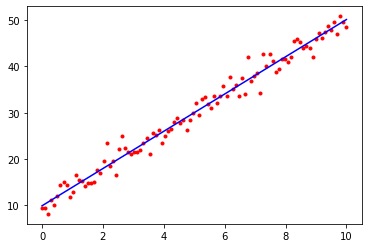
Exercise: Try to change the learning rate and see what happens.

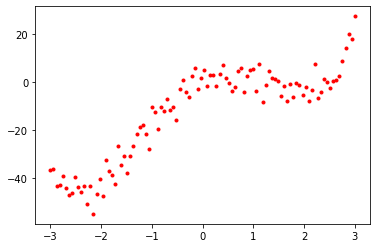
Exercise now try to fit the linear model to the data generated by the following model:

\[ t = x^4 - 10 x^2 + 10 x + \epsilon \]

where \(\epsilon \sim \mathcal{N}(0, 4)\).

# Generate synthetic data
N = 100  # Number of data points
x = np.linspace(-3, 3, N)  # Generate N values linearly-spaced between -3 and 3


t = x ** 4 - 10 * x ** 2 + 10 * x + np.random.normal(0, 4, x.shape[0])  # Generate corresponding targets
plt.plot(x, t, "r.")  # Plot data points

t = torch.from_numpy(t).view(-1, 1)

x = torch.from_numpy(x)
#t = torch.from_numpy(t)

# Initialize random parameters
w = torch.randn(1, requires_grad=True)
b = torch.randn(1, requires_grad=True)

# define cost function
def cost(w, b):
    y = w * x ** 4 + b
    return (1 / N) * torch.sum( (y - t) ** 2)


# Find the gradient of the cost function using pytorch
num_iterations = 100000 # Number of iterations
lr = 1e-6  # Learning rate

for i in range(num_iterations):

    # Evaluate the gradient of the current parameters stored in params
    loss = cost(w, b)
    loss.backward()

    if i % 100 == 0:
        print(f"i: {i:<5d} loss: {loss.item():.4f}")

    # Update parameters w and b
    with torch.no_grad():

        w.data = w - lr * w.grad
        b.data = b - lr * b.grad

        w.grad.zero_()  # we set the gradients to zero before the next iteration
        b.grad.zero_()

i: 0     loss: 97622.5119
i: 100   loss: 46004.2520
i: 200   loss: 45784.1475
i: 300   loss: 45569.6026
i: 400   loss: 45360.4767
i: 500   loss: 45156.6328
i: 600   loss: 44957.9377
i: 700   loss: 44764.2617
i: 800   loss: 44575.4765
i: 900   loss: 44391.4601
i: 1000  loss: 44212.0918
i: 1100  loss: 44037.2535
i: 1200  loss: 43866.8315
i: 1300  loss: 43700.7138
i: 1400  loss: 43538.7917
i: 1500  loss: 43380.9597
i: 1600  loss: 43227.1140
i: 1700  loss: 43077.1542
i: 1800  loss: 42930.9821
i: 1900  loss: 42788.5020
i: 2000  loss: 42649.6205
i: 2100  loss: 42514.2473
i: 2200  loss: 42382.2926
i: 2300  loss: 42253.6711
i: 2400  loss: 42128.2988
i: 2500  loss: 42006.0929
i: 2600  loss: 41886.9731
i: 2700  loss: 41770.8629
i: 2800  loss: 41657.6860
i: 2900  loss: 41547.3663
i: 3000  loss: 41439.8325
i: 3100  loss: 41335.0155
i: 3200  loss: 41232.8459
i: 3300  loss: 41133.2565
i: 3400  loss: 41036.1829
i: 3500  loss: 40941.5608
i: 3600  loss: 40849.3295
i: 3700  loss: 40759.4267
i: 3800  loss: 40671.7966
i: 3900  loss: 40586.3791
i: 4000  loss: 40503.1191
i: 4100  loss: 40421.9613
i: 4200  loss: 40342.8532
i: 4300  loss: 40265.7434
i: 4400  loss: 40190.5813
i: 4500  loss: 40117.3174
i: 4600  loss: 40045.9036
i: 4700  loss: 39976.2940
i: 4800  loss: 39908.4425
i: 4900  loss: 39842.3047
i: 5000  loss: 39777.8380
i: 5100  loss: 39714.9994
i: 5200  loss: 39653.7482
i: 5300  loss: 39594.0438
i: 5400  loss: 39535.8474
i: 5500  loss: 39479.1212
i: 5600  loss: 39423.8282
i: 5700  loss: 39369.9309
i: 5800  loss: 39317.3954
i: 5900  loss: 39266.1863
i: 6000  loss: 39216.2707
i: 6100  loss: 39167.6162
i: 6200  loss: 39120.1900
i: 6300  loss: 39073.9623
i: 6400  loss: 39028.9020
i: 6500  loss: 38984.9795
i: 6600  loss: 38942.1666
i: 6700  loss: 38900.4349
i: 6800  loss: 38859.7575
i: 6900  loss: 38820.1078
i: 7000  loss: 38781.4590
i: 7100  loss: 38743.7868
i: 7200  loss: 38707.0656
i: 7300  loss: 38671.2726
i: 7400  loss: 38636.3829
i: 7500  loss: 38602.3742
i: 7600  loss: 38569.2266
i: 7700  loss: 38536.9151
i: 7800  loss: 38505.4190
i: 7900  loss: 38474.7196
i: 8000  loss: 38444.7949
i: 8100  loss: 38415.6256
i: 8200  loss: 38387.1937
i: 8300  loss: 38359.4803
i: 8400  loss: 38332.4656
i: 8500  loss: 38306.1334
i: 8600  loss: 38280.4675
i: 8700  loss: 38255.4498
i: 8800  loss: 38231.0628
i: 8900  loss: 38207.2927
i: 9000  loss: 38184.1214
i: 9100  loss: 38161.5369
i: 9200  loss: 38139.5223
i: 9300  loss: 38118.0637
i: 9400  loss: 38097.1474
i: 9500  loss: 38076.7597
i: 9600  loss: 38056.8867
i: 9700  loss: 38037.5156
i: 9800  loss: 38018.6336
i: 9900  loss: 38000.2294
i: 10000 loss: 37982.2889
i: 10100 loss: 37964.8014
i: 10200 loss: 37947.7564
i: 10300 loss: 37931.1414
i: 10400 loss: 37914.9468
i: 10500 loss: 37899.1608
i: 10600 loss: 37883.7730
i: 10700 loss: 37868.7743
i: 10800 loss: 37854.1548
i: 10900 loss: 37839.9041
i: 11000 loss: 37826.0133
i: 11100 loss: 37812.4731
i: 11200 loss: 37799.2752
i: 11300 loss: 37786.4106
i: 11400 loss: 37773.8717
i: 11500 loss: 37761.6488
i: 11600 loss: 37749.7341
i: 11700 loss: 37738.1213
i: 11800 loss: 37726.8005
i: 11900 loss: 37715.7671
i: 12000 loss: 37705.0113
i: 12100 loss: 37694.5275
i: 12200 loss: 37684.3090
i: 12300 loss: 37674.3479
i: 12400 loss: 37664.6383
i: 12500 loss: 37655.1742
i: 12600 loss: 37645.9498
i: 12700 loss: 37636.9578
i: 12800 loss: 37628.1928
i: 12900 loss: 37619.6491
i: 13000 loss: 37611.3216
i: 13100 loss: 37603.2045
i: 13200 loss: 37595.2926
i: 13300 loss: 37587.5801
i: 13400 loss: 37580.0623
i: 13500 loss: 37572.7351
i: 13600 loss: 37565.5920
i: 13700 loss: 37558.6304
i: 13800 loss: 37551.8436
i: 13900 loss: 37545.2290
i: 14000 loss: 37538.7804
i: 14100 loss: 37532.4962
i: 14200 loss: 37526.3700
i: 14300 loss: 37520.3979
i: 14400 loss: 37514.5777
i: 14500 loss: 37508.9043
i: 14600 loss: 37503.3740
i: 14700 loss: 37497.9832
i: 14800 loss: 37492.7288
i: 14900 loss: 37487.6069
i: 15000 loss: 37482.6146
i: 15100 loss: 37477.7484
i: 15200 loss: 37473.0051
i: 15300 loss: 37468.3816
i: 15400 loss: 37463.8747
i: 15500 loss: 37459.4813
i: 15600 loss: 37455.1989
i: 15700 loss: 37451.0256
i: 15800 loss: 37446.9573
i: 15900 loss: 37442.9908
i: 16000 loss: 37439.1260
i: 16100 loss: 37435.3581
i: 16200 loss: 37431.6850
i: 16300 loss: 37428.1055
i: 16400 loss: 37424.6154
i: 16500 loss: 37421.2145
i: 16600 loss: 37417.8987
i: 16700 loss: 37414.6672
i: 16800 loss: 37411.5172
i: 16900 loss: 37408.4458
i: 17000 loss: 37405.4535
i: 17100 loss: 37402.5362
i: 17200 loss: 37399.6919
i: 17300 loss: 37396.9197
i: 17400 loss: 37394.2184
i: 17500 loss: 37391.5849
i: 17600 loss: 37389.0178
i: 17700 loss: 37386.5153
i: 17800 loss: 37384.0761
i: 17900 loss: 37381.6984
i: 18000 loss: 37379.3807
i: 18100 loss: 37377.1218
i: 18200 loss: 37374.9200
i: 18300 loss: 37372.7739
i: 18400 loss: 37370.6821
i: 18500 loss: 37368.6430
i: 18600 loss: 37366.6555
i: 18700 loss: 37364.7181
i: 18800 loss: 37362.8294
i: 18900 loss: 37360.9882
i: 19000 loss: 37359.1935
i: 19100 loss: 37357.4451
i: 19200 loss: 37355.7404
i: 19300 loss: 37354.0784
i: 19400 loss: 37352.4582
i: 19500 loss: 37350.8799
i: 19600 loss: 37349.3409
i: 19700 loss: 37347.8403
i: 19800 loss: 37346.3786
i: 19900 loss: 37344.9529
i: 20000 loss: 37343.5639
i: 20100 loss: 37342.2096
i: 20200 loss: 37340.8894
i: 20300 loss: 37339.6030
i: 20400 loss: 37338.3484
i: 20500 loss: 37337.1262
i: 20600 loss: 37335.9344
i: 20700 loss: 37334.7729
i: 20800 loss: 37333.6409
i: 20900 loss: 37332.5367
i: 21000 loss: 37331.4616
i: 21100 loss: 37330.4127
i: 21200 loss: 37329.3907
i: 21300 loss: 37328.3948
i: 21400 loss: 37327.4233
i: 21500 loss: 37326.4768
i: 21600 loss: 37325.5546
i: 21700 loss: 37324.6550
i: 21800 loss: 37323.7778
i: 21900 loss: 37322.9238
i: 22000 loss: 37322.0912
i: 22100 loss: 37321.2792
i: 22200 loss: 37320.4875
i: 22300 loss: 37319.7157
i: 22400 loss: 37318.9643
i: 22500 loss: 37318.2316
i: 22600 loss: 37317.5173
i: 22700 loss: 37316.8210
i: 22800 loss: 37316.1421
i: 22900 loss: 37315.4804
i: 23000 loss: 37314.8353
i: 23100 loss: 37314.2066
i: 23200 loss: 37313.5937
i: 23300 loss: 37312.9963
i: 23400 loss: 37312.4142
i: 23500 loss: 37311.8468
i: 23600 loss: 37311.2936
i: 23700 loss: 37310.7544
i: 23800 loss: 37310.2289
i: 23900 loss: 37309.7167
i: 24000 loss: 37309.2175
i: 24100 loss: 37308.7310
i: 24200 loss: 37308.2567
i: 24300 loss: 37307.7944
i: 24400 loss: 37307.3437
i: 24500 loss: 37306.9043
i: 24600 loss: 37306.4759
i: 24700 loss: 37306.0583
i: 24800 loss: 37305.6510
i: 24900 loss: 37305.2545
i: 25000 loss: 37304.8682
i: 25100 loss: 37304.4915
i: 25200 loss: 37304.1241
i: 25300 loss: 37303.7657
i: 25400 loss: 37303.4163
i: 25500 loss: 37303.0767
i: 25600 loss: 37302.7453
i: 25700 loss: 37302.4219
i: 25800 loss: 37302.1062
i: 25900 loss: 37301.7996
i: 26000 loss: 37301.5005
i: 26100 loss: 37301.2085
i: 26200 loss: 37300.9236
i: 26300 loss: 37300.6470
i: 26400 loss: 37300.3767
i: 26500 loss: 37300.1127
i: 26600 loss: 37299.8565
i: 26700 loss: 37299.6063
i: 26800 loss: 37299.3617
i: 26900 loss: 37299.1245
i: 27000 loss: 37298.8928
i: 27100 loss: 37298.6661
i: 27200 loss: 37298.4466
i: 27300 loss: 37298.2318
i: 27400 loss: 37298.0224
i: 27500 loss: 37297.8189
i: 27600 loss: 37297.6193
i: 27700 loss: 37297.4262
i: 27800 loss: 37297.2371
i: 27900 loss: 37297.0529
i: 28000 loss: 37296.8737
i: 28100 loss: 37296.6982
i: 28200 loss: 37296.5283
i: 28300 loss: 37296.3614
i: 28400 loss: 37296.2001
i: 28500 loss: 37296.0417
i: 28600 loss: 37295.8882
i: 28700 loss: 37295.7378
i: 28800 loss: 37295.5919
i: 28900 loss: 37295.4490
i: 29000 loss: 37295.3104
i: 29100 loss: 37295.1746
i: 29200 loss: 37295.0429
i: 29300 loss: 37294.9138
i: 29400 loss: 37294.7888
i: 29500 loss: 37294.6659
i: 29600 loss: 37294.5474
i: 29700 loss: 37294.4303
i: 29800 loss: 37294.3180
i: 29900 loss: 37294.2070
i: 30000 loss: 37294.0999
i: 30100 loss: 37293.9949
i: 30200 loss: 37293.8926
i: 30300 loss: 37293.7932
i: 30400 loss: 37293.6954
i: 30500 loss: 37293.6015
i: 30600 loss: 37293.5087
i: 30700 loss: 37293.4190
i: 30800 loss: 37293.3315
i: 30900 loss: 37293.2454
i: 31000 loss: 37293.1628
i: 31100 loss: 37293.0812
i: 31200 loss: 37293.0021
i: 31300 loss: 37292.9253
i: 31400 loss: 37292.8494
i: 31500 loss: 37292.7766
i: 31600 loss: 37292.7052
i: 31700 loss: 37292.6348
i: 31800 loss: 37292.5677
i: 31900 loss: 37292.5015
i: 32000 loss: 37292.4364
i: 32100 loss: 37292.3742
i: 32200 loss: 37292.3128
i: 32300 loss: 37292.2525
i: 32400 loss: 37292.1949
i: 32500 loss: 37292.1381
i: 32600 loss: 37292.0820
i: 32700 loss: 37292.0289
i: 32800 loss: 37291.9764
i: 32900 loss: 37291.9246
i: 33000 loss: 37291.8750
i: 33100 loss: 37291.8266
i: 33200 loss: 37291.7788
i: 33300 loss: 37291.7323
i: 33400 loss: 37291.6877
i: 33500 loss: 37291.6437
i: 33600 loss: 37291.6003
i: 33700 loss: 37291.5590
i: 33800 loss: 37291.5185
i: 33900 loss: 37291.4786
i: 34000 loss: 37291.4394
i: 34100 loss: 37291.4023
i: 34200 loss: 37291.3658
i: 34300 loss: 37291.3297
i: 34400 loss: 37291.2943
i: 34500 loss: 37291.2609
i: 34600 loss: 37291.2279
i: 34700 loss: 37291.1953
i: 34800 loss: 37291.1632
i: 34900 loss: 37291.1331
i: 35000 loss: 37291.1034
i: 35100 loss: 37291.0740
i: 35200 loss: 37291.0451
i: 35300 loss: 37291.0176
i: 35400 loss: 37290.9909
i: 35500 loss: 37290.9646
i: 35600 loss: 37290.9386
i: 35700 loss: 37290.9131
i: 35800 loss: 37290.8893
i: 35900 loss: 37290.8657
i: 36000 loss: 37290.8425
i: 36100 loss: 37290.8195
i: 36200 loss: 37290.7972
i: 36300 loss: 37290.7762
i: 36400 loss: 37290.7555
i: 36500 loss: 37290.7351
i: 36600 loss: 37290.7149
i: 36700 loss: 37290.6950
i: 36800 loss: 37290.6766
i: 36900 loss: 37290.6585
i: 37000 loss: 37290.6406
i: 37100 loss: 37290.6229
i: 37200 loss: 37290.6055
i: 37300 loss: 37290.5888
i: 37400 loss: 37290.5730
i: 37500 loss: 37290.5574
i: 37600 loss: 37290.5420
i: 37700 loss: 37290.5268
i: 37800 loss: 37290.5118
i: 37900 loss: 37290.4975
i: 38000 loss: 37290.4840
i: 38100 loss: 37290.4707
i: 38200 loss: 37290.4575
i: 38300 loss: 37290.4445
i: 38400 loss: 37290.4317
i: 38500 loss: 37290.4190
i: 38600 loss: 37290.4074
i: 38700 loss: 37290.3961
i: 38800 loss: 37290.3850
i: 38900 loss: 37290.3739
i: 39000 loss: 37290.3630
i: 39100 loss: 37290.3523
i: 39200 loss: 37290.3417
i: 39300 loss: 37290.3320
i: 39400 loss: 37290.3226
i: 39500 loss: 37290.3133
i: 39600 loss: 37290.3041
i: 39700 loss: 37290.2950
i: 39800 loss: 37290.2861
i: 39900 loss: 37290.2773
i: 40000 loss: 37290.2686
i: 40100 loss: 37290.2608
i: 40200 loss: 37290.2532
i: 40300 loss: 37290.2456
i: 40400 loss: 37290.2382
i: 40500 loss: 37290.2308
i: 40600 loss: 37290.2235
i: 40700 loss: 37290.2164
i: 40800 loss: 37290.2093
i: 40900 loss: 37290.2025
i: 41000 loss: 37290.1964
i: 41100 loss: 37290.1904
i: 41200 loss: 37290.1844
i: 41300 loss: 37290.1785
i: 41400 loss: 37290.1726
i: 41500 loss: 37290.1669
i: 41600 loss: 37290.1612
i: 41700 loss: 37290.1556
i: 41800 loss: 37290.1501
i: 41900 loss: 37290.1449
i: 42000 loss: 37290.1402
i: 42100 loss: 37290.1356
i: 42200 loss: 37290.1310
i: 42300 loss: 37290.1264
i: 42400 loss: 37290.1219
i: 42500 loss: 37290.1175
i: 42600 loss: 37290.1131
i: 42700 loss: 37290.1088
i: 42800 loss: 37290.1045
i: 42900 loss: 37290.1003
i: 43000 loss: 37290.0964
i: 43100 loss: 37290.0929
i: 43200 loss: 37290.0894
i: 43300 loss: 37290.0860
i: 43400 loss: 37290.0826
i: 43500 loss: 37290.0792
i: 43600 loss: 37290.0759
i: 43700 loss: 37290.0727
i: 43800 loss: 37290.0694
i: 43900 loss: 37290.0663
i: 44000 loss: 37290.0631
i: 44100 loss: 37290.0600
i: 44200 loss: 37290.0570
i: 44300 loss: 37290.0541
i: 44400 loss: 37290.0516
i: 44500 loss: 37290.0492
i: 44600 loss: 37290.0468
i: 44700 loss: 37290.0444
i: 44800 loss: 37290.0420
i: 44900 loss: 37290.0397
i: 45000 loss: 37290.0374
i: 45100 loss: 37290.0351
i: 45200 loss: 37290.0329
i: 45300 loss: 37290.0306
i: 45400 loss: 37290.0284
i: 45500 loss: 37290.0263
i: 45600 loss: 37290.0242
i: 45700 loss: 37290.0221
i: 45800 loss: 37290.0200
i: 45900 loss: 37290.0182
i: 46000 loss: 37290.0166
i: 46100 loss: 37290.0150
i: 46200 loss: 37290.0134
i: 46300 loss: 37290.0119
i: 46400 loss: 37290.0103
i: 46500 loss: 37290.0088
i: 46600 loss: 37290.0073
i: 46700 loss: 37290.0058
i: 46800 loss: 37290.0043
i: 46900 loss: 37290.0029
i: 47000 loss: 37290.0015
i: 47100 loss: 37290.0001
i: 47200 loss: 37289.9987
i: 47300 loss: 37289.9973
i: 47400 loss: 37289.9959
i: 47500 loss: 37289.9946
i: 47600 loss: 37289.9933
i: 47700 loss: 37289.9920
i: 47800 loss: 37289.9907
i: 47900 loss: 37289.9898
i: 48000 loss: 37289.9889
i: 48100 loss: 37289.9879
i: 48200 loss: 37289.9870
i: 48300 loss: 37289.9861
i: 48400 loss: 37289.9852
i: 48500 loss: 37289.9843
i: 48600 loss: 37289.9834
i: 48700 loss: 37289.9826
i: 48800 loss: 37289.9817
i: 48900 loss: 37289.9809
i: 49000 loss: 37289.9800
i: 49100 loss: 37289.9792
i: 49200 loss: 37289.9784
i: 49300 loss: 37289.9776
i: 49400 loss: 37289.9768
i: 49500 loss: 37289.9760
i: 49600 loss: 37289.9753
i: 49700 loss: 37289.9745
i: 49800 loss: 37289.9738
i: 49900 loss: 37289.9730
i: 50000 loss: 37289.9723
i: 50100 loss: 37289.9716
i: 50200 loss: 37289.9709
i: 50300 loss: 37289.9702
i: 50400 loss: 37289.9695
i: 50500 loss: 37289.9690
i: 50600 loss: 37289.9686
i: 50700 loss: 37289.9681
i: 50800 loss: 37289.9677
i: 50900 loss: 37289.9673
i: 51000 loss: 37289.9668
i: 51100 loss: 37289.9664
i: 51200 loss: 37289.9660
i: 51300 loss: 37289.9656
i: 51400 loss: 37289.9652
i: 51500 loss: 37289.9648
i: 51600 loss: 37289.9644
i: 51700 loss: 37289.9640
i: 51800 loss: 37289.9636
i: 51900 loss: 37289.9632
i: 52000 loss: 37289.9628
i: 52100 loss: 37289.9624
i: 52200 loss: 37289.9621
i: 52300 loss: 37289.9617
i: 52400 loss: 37289.9613
i: 52500 loss: 37289.9610
i: 52600 loss: 37289.9606
i: 52700 loss: 37289.9603
i: 52800 loss: 37289.9599
i: 52900 loss: 37289.9596
i: 53000 loss: 37289.9592
i: 53100 loss: 37289.9589
i: 53200 loss: 37289.9586
i: 53300 loss: 37289.9583
i: 53400 loss: 37289.9579
i: 53500 loss: 37289.9576
i: 53600 loss: 37289.9573
i: 53700 loss: 37289.9570
i: 53800 loss: 37289.9567
i: 53900 loss: 37289.9564
i: 54000 loss: 37289.9561
i: 54100 loss: 37289.9559
i: 54200 loss: 37289.9556
i: 54300 loss: 37289.9553
i: 54400 loss: 37289.9552
i: 54500 loss: 37289.9550
i: 54600 loss: 37289.9549
i: 54700 loss: 37289.9548
i: 54800 loss: 37289.9546
i: 54900 loss: 37289.9545
i: 55000 loss: 37289.9544
i: 55100 loss: 37289.9542
i: 55200 loss: 37289.9541
i: 55300 loss: 37289.9540
i: 55400 loss: 37289.9539
i: 55500 loss: 37289.9537
i: 55600 loss: 37289.9536
i: 55700 loss: 37289.9535
i: 55800 loss: 37289.9534
i: 55900 loss: 37289.9533
i: 56000 loss: 37289.9531
i: 56100 loss: 37289.9530
i: 56200 loss: 37289.9529
i: 56300 loss: 37289.9528
i: 56400 loss: 37289.9527
i: 56500 loss: 37289.9526
i: 56600 loss: 37289.9525
i: 56700 loss: 37289.9524
i: 56800 loss: 37289.9522
i: 56900 loss: 37289.9521
i: 57000 loss: 37289.9520
i: 57100 loss: 37289.9519
i: 57200 loss: 37289.9518
i: 57300 loss: 37289.9517
i: 57400 loss: 37289.9516
i: 57500 loss: 37289.9515
i: 57600 loss: 37289.9514
i: 57700 loss: 37289.9513
i: 57800 loss: 37289.9512
i: 57900 loss: 37289.9511
i: 58000 loss: 37289.9510
i: 58100 loss: 37289.9510
i: 58200 loss: 37289.9509
i: 58300 loss: 37289.9508
i: 58400 loss: 37289.9507
i: 58500 loss: 37289.9506
i: 58600 loss: 37289.9505
i: 58700 loss: 37289.9504
i: 58800 loss: 37289.9503
i: 58900 loss: 37289.9502
i: 59000 loss: 37289.9502
i: 59100 loss: 37289.9501
i: 59200 loss: 37289.9500
i: 59300 loss: 37289.9499
i: 59400 loss: 37289.9498
i: 59500 loss: 37289.9498
i: 59600 loss: 37289.9497
i: 59700 loss: 37289.9496
i: 59800 loss: 37289.9496
i: 59900 loss: 37289.9495
i: 60000 loss: 37289.9494
i: 60100 loss: 37289.9493
i: 60200 loss: 37289.9493
i: 60300 loss: 37289.9492
i: 60400 loss: 37289.9491
i: 60500 loss: 37289.9491
i: 60600 loss: 37289.9490
i: 60700 loss: 37289.9489
i: 60800 loss: 37289.9489
i: 60900 loss: 37289.9488
i: 61000 loss: 37289.9488
i: 61100 loss: 37289.9487
i: 61200 loss: 37289.9486
i: 61300 loss: 37289.9486
i: 61400 loss: 37289.9485
i: 61500 loss: 37289.9485
i: 61600 loss: 37289.9484
i: 61700 loss: 37289.9484
i: 61800 loss: 37289.9483
i: 61900 loss: 37289.9483
i: 62000 loss: 37289.9482
i: 62100 loss: 37289.9482
i: 62200 loss: 37289.9482
i: 62300 loss: 37289.9482
i: 62400 loss: 37289.9482
i: 62500 loss: 37289.9482
i: 62600 loss: 37289.9482
i: 62700 loss: 37289.9482
i: 62800 loss: 37289.9482
i: 62900 loss: 37289.9482
i: 63000 loss: 37289.9482
i: 63100 loss: 37289.9482
i: 63200 loss: 37289.9482
i: 63300 loss: 37289.9482
i: 63400 loss: 37289.9482
i: 63500 loss: 37289.9482
i: 63600 loss: 37289.9482
i: 63700 loss: 37289.9482
i: 63800 loss: 37289.9482
i: 63900 loss: 37289.9482
i: 64000 loss: 37289.9482
i: 64100 loss: 37289.9482
i: 64200 loss: 37289.9482
i: 64300 loss: 37289.9482
i: 64400 loss: 37289.9482
i: 64500 loss: 37289.9482
i: 64600 loss: 37289.9482
i: 64700 loss: 37289.9482
i: 64800 loss: 37289.9482
i: 64900 loss: 37289.9482
i: 65000 loss: 37289.9482
i: 65100 loss: 37289.9482
i: 65200 loss: 37289.9482
i: 65300 loss: 37289.9482
i: 65400 loss: 37289.9482
i: 65500 loss: 37289.9482
i: 65600 loss: 37289.9482
i: 65700 loss: 37289.9482
i: 65800 loss: 37289.9482
i: 65900 loss: 37289.9482
i: 66000 loss: 37289.9482
i: 66100 loss: 37289.9482
i: 66200 loss: 37289.9482
i: 66300 loss: 37289.9482
i: 66400 loss: 37289.9482
i: 66500 loss: 37289.9482
i: 66600 loss: 37289.9482
i: 66700 loss: 37289.9482
i: 66800 loss: 37289.9482
i: 66900 loss: 37289.9482
i: 67000 loss: 37289.9482
i: 67100 loss: 37289.9482
i: 67200 loss: 37289.9482
i: 67300 loss: 37289.9482
i: 67400 loss: 37289.9482
i: 67500 loss: 37289.9482
i: 67600 loss: 37289.9482
i: 67700 loss: 37289.9482
i: 67800 loss: 37289.9482
i: 67900 loss: 37289.9482
i: 68000 loss: 37289.9482
i: 68100 loss: 37289.9482
i: 68200 loss: 37289.9482
i: 68300 loss: 37289.9482
i: 68400 loss: 37289.9482
i: 68500 loss: 37289.9482
i: 68600 loss: 37289.9482
i: 68700 loss: 37289.9482
i: 68800 loss: 37289.9482
i: 68900 loss: 37289.9482
i: 69000 loss: 37289.9482
i: 69100 loss: 37289.9482
i: 69200 loss: 37289.9482
i: 69300 loss: 37289.9482
i: 69400 loss: 37289.9482
i: 69500 loss: 37289.9482
i: 69600 loss: 37289.9482
i: 69700 loss: 37289.9482
i: 69800 loss: 37289.9482
i: 69900 loss: 37289.9482
i: 70000 loss: 37289.9482
i: 70100 loss: 37289.9482
i: 70200 loss: 37289.9482
i: 70300 loss: 37289.9482
i: 70400 loss: 37289.9482
i: 70500 loss: 37289.9482
i: 70600 loss: 37289.9482
i: 70700 loss: 37289.9482
i: 70800 loss: 37289.9482
i: 70900 loss: 37289.9482
i: 71000 loss: 37289.9482
i: 71100 loss: 37289.9482
i: 71200 loss: 37289.9482
i: 71300 loss: 37289.9482
i: 71400 loss: 37289.9482
i: 71500 loss: 37289.9482
i: 71600 loss: 37289.9482
i: 71700 loss: 37289.9482
i: 71800 loss: 37289.9482
i: 71900 loss: 37289.9482
i: 72000 loss: 37289.9482
i: 72100 loss: 37289.9482
i: 72200 loss: 37289.9482
i: 72300 loss: 37289.9482
i: 72400 loss: 37289.9482
i: 72500 loss: 37289.9482
i: 72600 loss: 37289.9482
i: 72700 loss: 37289.9482
i: 72800 loss: 37289.9482
i: 72900 loss: 37289.9482
i: 73000 loss: 37289.9482
i: 73100 loss: 37289.9482
i: 73200 loss: 37289.9482
i: 73300 loss: 37289.9482
i: 73400 loss: 37289.9482
i: 73500 loss: 37289.9482
i: 73600 loss: 37289.9482
i: 73700 loss: 37289.9482
i: 73800 loss: 37289.9482
i: 73900 loss: 37289.9482
i: 74000 loss: 37289.9482
i: 74100 loss: 37289.9482
i: 74200 loss: 37289.9482
i: 74300 loss: 37289.9482
i: 74400 loss: 37289.9482
i: 74500 loss: 37289.9482
i: 74600 loss: 37289.9482
i: 74700 loss: 37289.9482
i: 74800 loss: 37289.9482
i: 74900 loss: 37289.9482
i: 75000 loss: 37289.9482
i: 75100 loss: 37289.9482
i: 75200 loss: 37289.9482
i: 75300 loss: 37289.9482
i: 75400 loss: 37289.9482
i: 75500 loss: 37289.9482
i: 75600 loss: 37289.9482
i: 75700 loss: 37289.9482
i: 75800 loss: 37289.9482
i: 75900 loss: 37289.9482
i: 76000 loss: 37289.9482
i: 76100 loss: 37289.9482
i: 76200 loss: 37289.9482
i: 76300 loss: 37289.9482
i: 76400 loss: 37289.9482
i: 76500 loss: 37289.9482
i: 76600 loss: 37289.9482
i: 76700 loss: 37289.9482
i: 76800 loss: 37289.9482
i: 76900 loss: 37289.9482
i: 77000 loss: 37289.9482
i: 77100 loss: 37289.9482
i: 77200 loss: 37289.9482
i: 77300 loss: 37289.9482
i: 77400 loss: 37289.9482
i: 77500 loss: 37289.9482
i: 77600 loss: 37289.9482
i: 77700 loss: 37289.9482
i: 77800 loss: 37289.9482
i: 77900 loss: 37289.9482
i: 78000 loss: 37289.9482
i: 78100 loss: 37289.9482
i: 78200 loss: 37289.9482
i: 78300 loss: 37289.9482
i: 78400 loss: 37289.9482
i: 78500 loss: 37289.9482
i: 78600 loss: 37289.9482
i: 78700 loss: 37289.9482
i: 78800 loss: 37289.9482
i: 78900 loss: 37289.9482
i: 79000 loss: 37289.9482
i: 79100 loss: 37289.9482
i: 79200 loss: 37289.9482
i: 79300 loss: 37289.9482
i: 79400 loss: 37289.9482
i: 79500 loss: 37289.9482
i: 79600 loss: 37289.9482
i: 79700 loss: 37289.9482
i: 79800 loss: 37289.9482
i: 79900 loss: 37289.9482
i: 80000 loss: 37289.9482
i: 80100 loss: 37289.9482
i: 80200 loss: 37289.9482
i: 80300 loss: 37289.9482
i: 80400 loss: 37289.9482
i: 80500 loss: 37289.9482
i: 80600 loss: 37289.9482
i: 80700 loss: 37289.9482
i: 80800 loss: 37289.9482
i: 80900 loss: 37289.9482
i: 81000 loss: 37289.9482
i: 81100 loss: 37289.9482
i: 81200 loss: 37289.9482
i: 81300 loss: 37289.9482
i: 81400 loss: 37289.9482
i: 81500 loss: 37289.9482
i: 81600 loss: 37289.9482
i: 81700 loss: 37289.9482
i: 81800 loss: 37289.9482
i: 81900 loss: 37289.9482
i: 82000 loss: 37289.9482
i: 82100 loss: 37289.9482
i: 82200 loss: 37289.9482
i: 82300 loss: 37289.9482
i: 82400 loss: 37289.9482
i: 82500 loss: 37289.9482
i: 82600 loss: 37289.9482
i: 82700 loss: 37289.9482
i: 82800 loss: 37289.9482
i: 82900 loss: 37289.9482
i: 83000 loss: 37289.9482
i: 83100 loss: 37289.9482
i: 83200 loss: 37289.9482
i: 83300 loss: 37289.9482
i: 83400 loss: 37289.9482
i: 83500 loss: 37289.9482
i: 83600 loss: 37289.9482
i: 83700 loss: 37289.9482
i: 83800 loss: 37289.9482
i: 83900 loss: 37289.9482
i: 84000 loss: 37289.9482
i: 84100 loss: 37289.9482
i: 84200 loss: 37289.9482
i: 84300 loss: 37289.9482
i: 84400 loss: 37289.9482
i: 84500 loss: 37289.9482
i: 84600 loss: 37289.9482
i: 84700 loss: 37289.9482
i: 84800 loss: 37289.9482
i: 84900 loss: 37289.9482
i: 85000 loss: 37289.9482
i: 85100 loss: 37289.9482
i: 85200 loss: 37289.9482
i: 85300 loss: 37289.9482
i: 85400 loss: 37289.9482
i: 85500 loss: 37289.9482
i: 85600 loss: 37289.9482
i: 85700 loss: 37289.9482
i: 85800 loss: 37289.9482
i: 85900 loss: 37289.9482
i: 86000 loss: 37289.9482
i: 86100 loss: 37289.9482
i: 86200 loss: 37289.9482
i: 86300 loss: 37289.9482
i: 86400 loss: 37289.9482
i: 86500 loss: 37289.9482
i: 86600 loss: 37289.9482
i: 86700 loss: 37289.9482
i: 86800 loss: 37289.9482
i: 86900 loss: 37289.9482
i: 87000 loss: 37289.9482
i: 87100 loss: 37289.9482
i: 87200 loss: 37289.9482
i: 87300 loss: 37289.9482
i: 87400 loss: 37289.9482
i: 87500 loss: 37289.9482
i: 87600 loss: 37289.9482
i: 87700 loss: 37289.9482
i: 87800 loss: 37289.9482
i: 87900 loss: 37289.9482
i: 88000 loss: 37289.9482
i: 88100 loss: 37289.9482
i: 88200 loss: 37289.9482
i: 88300 loss: 37289.9482
i: 88400 loss: 37289.9482
i: 88500 loss: 37289.9482
i: 88600 loss: 37289.9482
i: 88700 loss: 37289.9482
i: 88800 loss: 37289.9482
i: 88900 loss: 37289.9482
i: 89000 loss: 37289.9482
i: 89100 loss: 37289.9482
i: 89200 loss: 37289.9482
i: 89300 loss: 37289.9482
i: 89400 loss: 37289.9482
i: 89500 loss: 37289.9482
i: 89600 loss: 37289.9482
i: 89700 loss: 37289.9482
i: 89800 loss: 37289.9482
i: 89900 loss: 37289.9482
i: 90000 loss: 37289.9482
i: 90100 loss: 37289.9482
i: 90200 loss: 37289.9482
i: 90300 loss: 37289.9482
i: 90400 loss: 37289.9482
i: 90500 loss: 37289.9482
i: 90600 loss: 37289.9482
i: 90700 loss: 37289.9482
i: 90800 loss: 37289.9482
i: 90900 loss: 37289.9482
i: 91000 loss: 37289.9482
i: 91100 loss: 37289.9482
i: 91200 loss: 37289.9482
i: 91300 loss: 37289.9482
i: 91400 loss: 37289.9482
i: 91500 loss: 37289.9482
i: 91600 loss: 37289.9482
i: 91700 loss: 37289.9482
i: 91800 loss: 37289.9482
i: 91900 loss: 37289.9482
i: 92000 loss: 37289.9482
i: 92100 loss: 37289.9482
i: 92200 loss: 37289.9482
i: 92300 loss: 37289.9482
i: 92400 loss: 37289.9482
i: 92500 loss: 37289.9482
i: 92600 loss: 37289.9482
i: 92700 loss: 37289.9482
i: 92800 loss: 37289.9482
i: 92900 loss: 37289.9482
i: 93000 loss: 37289.9482
i: 93100 loss: 37289.9482
i: 93200 loss: 37289.9482
i: 93300 loss: 37289.9482
i: 93400 loss: 37289.9482
i: 93500 loss: 37289.9482
i: 93600 loss: 37289.9482
i: 93700 loss: 37289.9482
i: 93800 loss: 37289.9482
i: 93900 loss: 37289.9482
i: 94000 loss: 37289.9482
i: 94100 loss: 37289.9482
i: 94200 loss: 37289.9482
i: 94300 loss: 37289.9482
i: 94400 loss: 37289.9482
i: 94500 loss: 37289.9482
i: 94600 loss: 37289.9482
i: 94700 loss: 37289.9482
i: 94800 loss: 37289.9482
i: 94900 loss: 37289.9482
i: 95000 loss: 37289.9482
i: 95100 loss: 37289.9482
i: 95200 loss: 37289.9482
i: 95300 loss: 37289.9482
i: 95400 loss: 37289.9482
i: 95500 loss: 37289.9482
i: 95600 loss: 37289.9482
i: 95700 loss: 37289.9482
i: 95800 loss: 37289.9482
i: 95900 loss: 37289.9482
i: 96000 loss: 37289.9482
i: 96100 loss: 37289.9482
i: 96200 loss: 37289.9482
i: 96300 loss: 37289.9482
i: 96400 loss: 37289.9482
i: 96500 loss: 37289.9482
i: 96600 loss: 37289.9482
i: 96700 loss: 37289.9482
i: 96800 loss: 37289.9482
i: 96900 loss: 37289.9482
i: 97000 loss: 37289.9482
i: 97100 loss: 37289.9482
i: 97200 loss: 37289.9482
i: 97300 loss: 37289.9482
i: 97400 loss: 37289.9482
i: 97500 loss: 37289.9482
i: 97600 loss: 37289.9482
i: 97700 loss: 37289.9482
i: 97800 loss: 37289.9482
i: 97900 loss: 37289.9482
i: 98000 loss: 37289.9482
i: 98100 loss: 37289.9482
i: 98200 loss: 37289.9482
i: 98300 loss: 37289.9482
i: 98400 loss: 37289.9482
i: 98500 loss: 37289.9482
i: 98600 loss: 37289.9482
i: 98700 loss: 37289.9482
i: 98800 loss: 37289.9482
i: 98900 loss: 37289.9482
i: 99000 loss: 37289.9482
i: 99100 loss: 37289.9482
i: 99200 loss: 37289.9482
i: 99300 loss: 37289.9482
i: 99400 loss: 37289.9482
i: 99500 loss: 37289.9482
i: 99600 loss: 37289.9482
i: 99700 loss: 37289.9482
i: 99800 loss: 37289.9482
i: 99900 loss: 37289.9482

b_numpy = b.detach().numpy()
w_numpy = w.detach().numpy()

plt.plot(x, t, "r.")
plt.plot([-2, 10], [b_numpy, w_numpy * 10 + b_numpy], "b-")

[<matplotlib.lines.Line2D at 0x15e8782b0>]

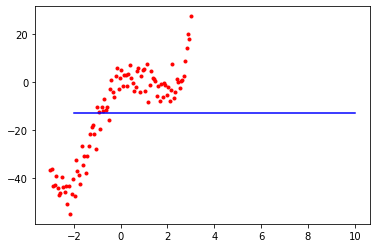
Exercise: Automatic Differentiation in Finance: call option pricing and derivatives

Let’s consider the following model for the price of a call option, which uses the Black-Scholes formula, with the following variables:

• \(K\) is the strike price of the option

• \(S_t\) is the price of the underlying asset at time \(t\)

• \(t\) is the current time in years

• \(T\) time of option expiration in years

• \(\sigma\) is the standard deviation of the asset returns

• \(r\) is the risk-free interest rate (annualized)

• \(N(x)\) is the cumulative distribution function of the standard normal distribution

\[ C(S_t, t) = N(d_1) S_t - N(d_2) K e^{-r(T-t)} \]

\[ d_1 = \frac{1}{\sigma\sqrt{T-t}}[\ln(\frac{S_t}{K}) + (r + \frac{\sigma^2}{2})(T-t)] \]

\[ d_2 = d_1 - \sigma\sqrt{T-t} \]

1. Implement the previous function to compute the price C of a call option:

from torch.distributions import Normal
import torch

std_norm_cdf = Normal(0, 1).cdf   # you can use this for the cdf of the standard normal distribution

def call_option_price_(K, S, T, sigma, r):
    d1 = 1 / (sigma*torch.sqrt(T)) * (torch.log(S/K) + (r + 0.5*sigma**2)*T)
    d2 = d1 - sigma*torch.sqrt(T)
    price = std_norm_cdf(d1)*S - std_norm_cdf(d2)*K*torch.exp(-r*T)
    return price

# this is the same as the previous one, it does not matter if we use auxiliary variables
def call_option_price(K, S, T, sigma, r):
    d1 = 1 / (sigma*torch.sqrt(T)) * (torch.log(S/K) + (r + 0.5*sigma**2)*T)
    price = std_norm_cdf(d1)*S - std_norm_cdf(d1 - sigma*torch.sqrt(T))*K*torch.exp(-r*T)
    return price

2. Calculate the price of a call option with the underyling at 100, strike price at 100, 1 year to expiration, 5% annual volatility, and a risk-free rate of 1% annually.

S = torch.tensor(100)
K = torch.tensor(100)
T = torch.tensor(1)
sigma = torch.tensor(0.05)
r = torch.tensor(0.01)

price = call_option_price(K=K, S=S, T=T, sigma=sigma, r=r)
price

tensor(2.5216)

The greeks are the partial derivatives of the option price with respect to the different parameters. They are used to hedge the risk of the option.

https://en.wikipedia.org/wiki/Greeks_(finance)

3. Compute the greeks Delta, Vega, Theta and Rho for the previous values of the option.

S = torch.tensor(100.0, requires_grad=True)
K = torch.tensor(100.0, requires_grad=True)
T = torch.tensor(1.0, requires_grad=True)
sigma = torch.tensor(0.05, requires_grad=True)
r = torch.tensor(0.01, requires_grad=True)

price = call_option_price(K=K, S=S, T=T, sigma=sigma, r=r)


price.backward()

print("Delta:", S.grad)
print(K.grad)
print(T.grad)
print(sigma.grad)
print(r.grad)

Delta: tensor(0.5890)
tensor(-0.5638)
tensor(1.5362)
tensor(38.8971)
tensor(56.3794)